Answer:
1.
 where
where
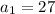
2.
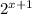
3. The domain is {-12,-8,0,1}. The range is {0,12,8}.
Explanation:
1. The recursive formula is defined as an implicit way of writing the rule of a function or pattern. It is implicit because it uses previous terms to find the next term in the pattern. We multiply, add, subtract or divide a previous term by a constant value or expression to find the next. In this case, 27 becomes 9 through division by 3 or multiplication by 1/3. The pattern continues 9(1/3)=3 and so forth.
2. The function f(x) is an exponential and has a general form of
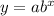 . We know f(x) is
. We know f(x) is
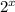 . The points of g(x) all changed from f(x) by shifting over to the left. This transformation occurred by
. The points of g(x) all changed from f(x) by shifting over to the left. This transformation occurred by
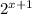 .
.
3. Domain is defined as the set of all x-values. Range is defined as the set of all y-values. The domain is {-12,-8,0,1}. The range is {0,12,8}.