Answer:
(x+1) is a factor with remainder 0.
Explanation:
We divide (x+1) into the polynomial
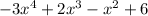 through long division or synthetic. We choose long division and look for what will multiply with (x+1) to make the polynomial
through long division or synthetic. We choose long division and look for what will multiply with (x+1) to make the polynomial
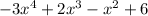 .
.
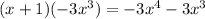
We subtract this from the original
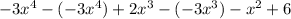 .
.
This leaves
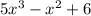 . We repeat the step above.
. We repeat the step above.
 .
.
We subtract this from
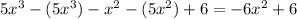 . We repeat the step above.
. We repeat the step above.
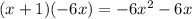 .
.
We subtract this from
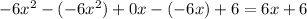 . We repeat the step above.
. We repeat the step above.
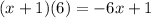 .
.
We subtract this from
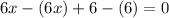 . There is no remainder. This means (x+1) is a factor.
. There is no remainder. This means (x+1) is a factor.