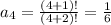Answer:
The correct answer option is:
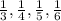 .
.
Explanation:
We know that the
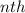 term
term
 for an arithmetic sequence is given by:
for an arithmetic sequence is given by:
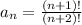
where
 is the number of the position of the term.
is the number of the position of the term.
We are supposed to find the first four terms of the sequence so we will substitute the values of
 from 1 to 4 in the given formula to get:
from 1 to 4 in the given formula to get:
1st term:
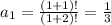
2nd term:
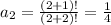
3rd term:
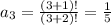
4th term: