Question

which equation results from isolating a radical term and squaring both sides of the equation for the equation

Answer 1

D.
`c-2=25+c+10√(c)`

Step-by-step explanation:

We have been given a radical equation
`√(c-2)-√(c)=5`. We are asked to find the equation that results from isolating a radical term and squaring both sides of the equation for the equation.

Add
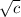`√(c)` on both sides:

`√(c-2)-√(c)+√(c)=5+√(c)`

`√(c-2)=5+√(c)`

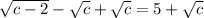
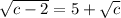
Square both sides:

`(√(c-2))^2=(5+√(c))^2`

Using radical rule
`\sqrt[n]{a^n} =a`, we will get:

`c-2=(5+√(c))^2`

Using perfect square formula
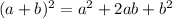`(a+b)^2=a^2+2ab+b^2`, we will get:

`c-2=5^2+2*5√(c)+(√(c))^2`

`c-2=25+10√(c)+c`

`c-2=25+c+10√(c)`

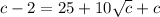
Therefore, option D is the correct choice.

Answer 2

D) c - 2 = 25 + c + 10√c

Explanation:

The given equation is
`√(c - 2) - √(c)  = 5`

`√(c -2) = 5 + √(c) \\`

Taking square on both sides, we get

Here we used ( a+ b)^2 = a^2 + b^2 + 2ab formula.

c - 2 = 5^2 + (√c)^2 + 2(5)√c

c - 2 = 25 + c +10√c

Answer: D) c - 2 = 25 + c + 10√c

Thank you.