Question

The rectangle below has an area of x^2-6x-7x 2 ?6x?7 square meters and a width of x-7x?7 meters. What expression represents the length of the rectangle?

Answer 1

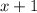`x+1` meters.

Explanation:

Let L be the length of rectangle.

We have been given that the rectangle has an area of
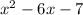`x^(2)-6x-7` square meters and a width of
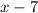`x-7` meters.

Since we know that area of rectangle is the product of its length and width.

`\text{Area of rectangle}=\text{Width* Length}`

`\text{ Length}=\frac{\text{Area of rectangle}}{\text{Width}}`

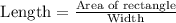
To find the length of our given rectangle we will divide area of rectangle by width of our rectangle.

`L=(x^2-6x-7)/(x-7)`

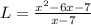
Let us factor out our numerator by splitting the middle term.

`L=(x^2-7x+x-7)/(x-7)`

`L=(x(x-7)+1(x-7))/(x-7)`

`L=((x-7)(x+1))/(x-7)`

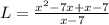
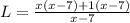
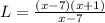
Upon cancelling out x-7 from numerator and denominator we will get,

`L=(x+1)`

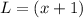
Therefore, the length of our rectangle will be
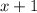`x+1` meters.