Question

Please help ASAP!!!

A group of athletic people were asked whether they played soccer or basketball. The table shows the probabilities of results.

Answer 1

C

Explanation:

Answer 2

C. Playing soccer and basketball are not independent since P(soccer|basketball) ≠ P(soccer) and P(basketball|soccer) ≠ P(basketball) .

Explanation:

We have the data of athletic people that played soccer and basketball.

Let, P(A) = probability of people who played soccer

P(B) = probability of people who played basketball

P(A∩B) = probability of people who played both soccer and basketball.

We will now find the probability of soccer | basketball

i.e.
`P(A|B)=(P(A \bigcap B))/(P(B))`

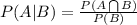
i.e.
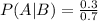`P(A|B)=(0.3)/(0.7)` = i.e.
`P(A|B)=0.43`

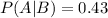
As,
`P(A|B)=0.43` ≠
`P(B)=0.7`

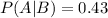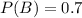
So, options A, B and D are discarded.

Moreover, i.e.
`P(B|A)=(P(B \bigcap A))/(P(A))`

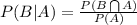
i.e.
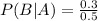`P(B|A)=(0.3)/(0.5)` = i.e.
`P(B|A)=0.375`

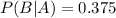
i.e.
`P(B|A)=0.375` ≠
`P(A)=0.5`

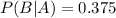Hence, we get that playing soccer and basketball are not independent.