Question

What is the equation of the line that passes through the points (-3,2) and (-5,8)

a. 3x - y = -11
b. 3x + y = -7
c. 3x + y = 5
d. x + 3y = 4

Answer 1

Greetings!

Answer:

The answer is a. 3x - y = -11

Explanation:

Firstly, you must find the gradient. This is found using the following formula:

`(y2 - y1)/(x2 - x1)`

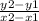
Make sure that the x2 and y2 values are in the same coordinate set:

Let's set (-3 , 2) as y1 and x1,

y1 = 2 and x1 = -3

That means that (-5 , 8) is y2 and x2,

y2 = 8 and x2 = -5

Plug the values in:

`(8 - 2)/(-5 - - 3)`

Simplified:

`(6)/(2)`

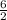
Or 3

So the gradient (or slope) is 3

Now, using the following equation of a line formula:

y - y1 = m(x - x1)

Where m is the gradient and y1 and x1 are two coordinates, we can plug these values in:

y1 = 2

x1 = -3

m = 3

y - 2 = 3(x - - 3)

The negative and the subtract makes it a positive:

y - 2 = 3(x + 3)

Now we can multiply the bracket out:

3 * x = 3x

3 * 3 = 9

So:

y - 2 = 3x + 9

The equation is usually in the form:

y = mx + c

So we need to move the -2 over to the other side making it a positive 2:

y = 3x + 9 + 2

y = 3x + 11

Which is the equation of the line.

The one option that this rearranges to is a) because if you move the y over to the 3x, and the + 11 over to the other side, making them both negatives, the result is:

3x - y = -11

So your answer is a.

Hope this helps!