Question

Which of the following is equivalent to (1/2)^-2t

Answer 1

The correct answer option is
`(2^2)^t`.

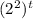Explanation:

We are given the following expression and we are to tell whether which of the given options is it equivalent to:

`((1)/(2))^{-2t)`

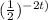
If we look at the first option
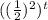`(((1)/(2) )^2)^t`, the power is going to be positive here.

The second option will be equal to
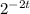`2^(-2t)` and not
`((1)/(2))^{-2t)`.

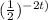While the third option is the correct one:
`(2^2)^t`.

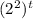When the 2 is shifted to the denominator, its power becomes negative and so it becomes equivalent to
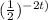`((1)/(2))^{-2t)`.

Answer 2

Choice (3)
`\left(2^2\right)^t` is correct.

Explanation:

Given expression is
`\left((1)/(2)\right)^(-2t)`

Now we need to simplify this and check which of the given choices best match with it.

`\left((1)/(2)\right)^(-2t)`

`=\left((1)/(2^1)\right)^(-2t)`

`=\left(2^(-1)\right)^(-2t)` {using formula
`=(1)/(x^m)=x^(-m)`}

`=\left(2^(-1)\right)^(-2t)` {using formula
`=\left(x^m\right)^n=x^(\left(m\cdot n\right))`}

`=2^(\left(-1\right)\left(-2t\right))`

`=2^(2t)`

`=\left(2^2\right)^t` {using formula
`=\left(x^m\right)^n=x^(\left(m\cdot n\right))`}

Hence choice (3)
`\left(2^2\right)^t` is correct.