Question

Answer the question for each scenario by applying the rule of 72. How many years will it take each situation to double its money? Situation A: Matthew invests $5,000 in an account with a compound interest rate of 12%. Situation B: Morgan invests $2,500 in an account with a compound interest rate of 8%. Situation C: Maysen invests $10,000 in an account with a compound interest rate of 4.5%. Whose money will double fastest?

Answer 1

Explanation:

Situation A: 6

Situation B: 9

Situation C: 16

Whose money will double the fastest?

-Matthew's

Answer 2

Matthew's money will double fastest in 6 years.

Explanation:

In this question we have to calculate, how many years it will take each situation to double its money by the rule of 72.

formula =
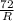`(72)/(R)` where R = Rate of interest

Situation A :

Matthew invests $5,000 in an account with a compound interest rate of 12%.

So
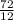`(72)/(12)` = 6 years

It will take 6 years to double the investment.

Situation B :

Morgan invests $2,500 in an account with a compound interest rate of 8%.

So
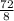`(72)/(8)` = 9 years

It will take 9 years to double the investment.

Situation C :

Maysen invests 10,000 in an account with a compound interest rate of 4.5%

So
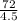`(72)/(4.5)` = 16 years

It will take 16 years to double the investment.

Matthew's money will double fastest in 6 years.