Question

Parallelogram ABCD has vertices at A(2,-3), B(8,-6), Cl14,-3), and D(8,0)

IF THE FOLLOWING STATEMENTS ARE TRUE, WHAT KIND OF PARALLELOGRAM IS THIS

The lengths of two consecutive sides are equal.

The slopes of two consecutive sides are not opposite reciprocals.

A) rectangle
B) square
C)rhombus
D) not enough info

Answer 1

The correct option is C.

Explanation:

The vertices of ABCD are A(2,-3), B(8,-6), C(14,-3), and D(8,0).

Distance formula:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

The length of sides are

`AB=√((8-2)^2+(-6+3)^2)=√(36+9)=√(45)`

`BC=√((14-8)^2+(-3+6)^2)=√(36+9)=√(45)`

`CD=√((8-14)^2+(0-3)^2)=√(36+9)=√(45)`

`AD=√((8-2)^2+(0+3)^2)=√(36+9)=√(45)`

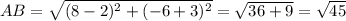
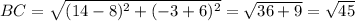
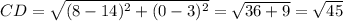
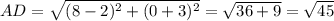
Since length of all sides are equation therefore the given parallelogram cannot be a rectangle.

Slope formula:

`m=(y_2-y_1)/(x_2-x_1)`

Slope of AB is

`m_1=(-6-(-3))/(8-2)=(-3)/(6)=(-1)/(2)`

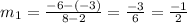
Slope of BC is

`m_2=(-3-(-6))/(14-8)=(3)/(6)=(1)/(2)`

Since the slopes of two consecutive sides are not opposite reciprocals, therefore the given parallelogram is a rhombus. Option C is correct.