Answer:
The length of the arc on the sixth swing was 12.18 ft.
Explanation:
A rope is swinging in such a way that the length of the arc traced by a knot at its bottom end is decreasing geometrically.
The third arc is 22 ft. long and the seventh arc is 10 ft.
Hence, the 3rd term is 22 and 7th term is 10.
The length of the arc on the sixth swing is asked, so we have to calculate the 6th term.
We know the nth term in GP is,
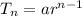
So,
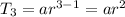 ----------------1
----------------1
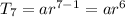 ----------------2
----------------2
Dividing equation 2 by 1,
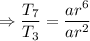
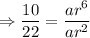


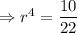
![\Rightarrow r=\sqrt[4]{(10)/(22)}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/ph2jix1bnar4jd06zfhwqchik5l2he678a.png)

Then the 6th term will be,
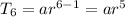 ----------------3
----------------3
Dividing equation 2 by 3,
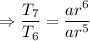
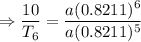
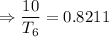
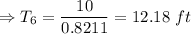
Therefore, the length of the arc on the sixth swing was 12.18 ft.