Question

Write the first five terms of the sequence in which the nth term is

Answer 1

Third option 2,6,24,120,720

Explanation:

Step 1

The first step is to simplify the expression for the nth term of this sequence using the definition of the factorial symbol. The simplification of this expression is done below,

`a_n=((n+2)!)/((n+2))=((n+2)*(n+1)!)/((n+2)) =(n+1)!`

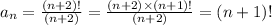
Step 2

The second step is to use the substitute different values of n into the expression of the nth term to work out which sequence corresponds to the correct answer.

`a_1=(1+1)!=2!=2\\a_2=(2+1)!=3!=6\\a_3=(3+1)!=4!=24\\a_4=(4+1)!=5!=120\\a_5=(5+1)!=6!=720`

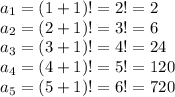
The terms of the sequence are {2,6,24,120,720}. The correct answer is the third option.