Question

To win the game, a place kicker must kick a

football from a point 24 m (26.2464 yd) from
the goal, and the ball must clear the crossbar,
which is 3.05 m high. When kicked, the ball
leaves the ground with a speed of 17 m/s at
an angle of 53.8
◦
from the horizontal.
The acceleration of gravity is 9.8 m/s
2
.
By how much vertical distance does the ball
clear the crossbar?
Answer in units of m

Answer 1

1.42 m

Step-by-step explanation:

Let's first write down the data given

We have

• 
  `\Delta{$x$} $ = horizontal distance from the kickoff point to goal = 24 $m`
• 
  `h$ = height of the crossbar = 3.05 m`
• 
  `\theta$ = angle at which the ball leaves the ground = 53,8^(\circ)`
• 
  `v = 17 m/s`
• 
  `g = $ acceleration due to gravity = -9.8 m/s^2`.
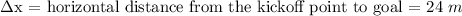
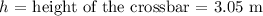
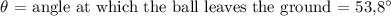
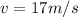
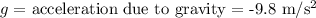  Note that we take g to -9.8 m/s² since gravity is acting in the opposite direction to the vertical movement of the ball. Thus the ball is slowing down with increasing height

The horizontal component of the velocity

`v_x= $v\cos(53.8) = 17 (0.59) = 10.04 $ m/s`

Time t, taken to traverse distance of 24m = Δx/vx = 24/10.04 = 2.39s

The vertical component of velocity

`v_y =v\cdot\sin(53^(\circ))\\= 13.58m/s`

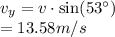
The vertical displacement is given by

`\Delta y = v_yt + (1)/(2)gt^2\\\\= 13.58 * 2.39 - (1)/(2) * 9.8 * 2.39^2\\\\= 4.46691 m`

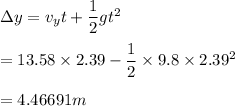
Since the height of the cross bar is 3.05m, the ball clears the crossbar by 4.46691 - 3.05 = 1.41691 ≈ 1.42 m