Question

Cynthia wants to take out a $8500 loan with a 4.75% APR. She can afford to pay $245 per month for loan payments. How long should he borrow the money so that she can afford the monthly payment?

Answer 1

She should borrow the money for 3.1161... years so that she can afford the monthly payment.

Explanation:

Monthly payment formula is:
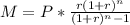`M=P*(r(1+r)^n)/((1+r)^n -1)` , where

M = Monthly payment amount, P = Loan amount, r = rate of interest per month and n = total number of months.

Given that, Cynthia wants to take out a $8500 loan with a 4.75% APR and she can afford to pay $245 per month.

That means,
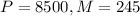`P= 8500, M= 245` and
`r= (0.0475)/(12)= 0.0039583`

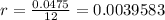
Plugging these values into the above formula, we will get........

`245=8500*(0.0039583(1+0.0039583)^n)/((1+0.0039583)^n-1) \\ \\ 245=(33.64555(1.0039583)^n)/((1.0039583)^n -1)\\ \\ 245(1.0039583)^n -245=33.64555(1.0039583)^n\\ \\ 211.35445(1.0039583)^n=245\\ \\ (1.0039583)^n=(245)/(211.35445)=1.15919\\ \\ n= log_(1.0039583)(1.15919)=37.39327`

So,
`n= 37.39327 months =(37.39327)/(12) years = 3.1161... years`

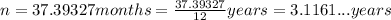
That means, she should borrow the money for 3.1161... years so that she can afford the monthly payment.