Question

Lim
x->infinity (1+1/n)

Answer 1

`^( \lim)_(n \to \infty) (1+(1)/(n))=1`

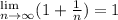
Explanation:

We want to evaluate the following limit.

`^( \lim)_(n \to \infty) (1+(1)/(n))`

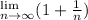
We need to recall that, limit of a sum is the sum of the limit.

So we need to find each individual limit and add them up.

`^( \lim)_(n \to \infty) (1+(1)/(n))=^( \lim)_(n \to \infty) (1) +^( \lim)_(n \to \infty) (1)/(n)`

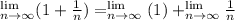
Recall that, as
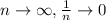`n\rightarrow \infty,(1)/(n) \rightarrow 0` and the limit of a constant, gives the same constant value.

This implies that,

`^( \lim)_(n \to \infty) (1+(1)/(n))= 1 +0`

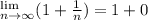
This gives us,

`^( \lim)_(n \to \infty) (1+(1)/(n))= 1`

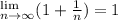
The correct answer is D