Answer:
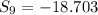 .
.
Explanation:
The given series is,
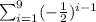
When we substitute
 , we get the first term, which is
, we get the first term, which is
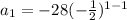
This implies that,
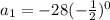
 .
.
The common ratio is
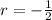
The finite geometric sum is given by the formula,
 .
.
Since there are 9 terms, we find the sum of the first nine terms by putting
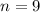 in to the formula to get,
in to the formula to get,
 .
.
 .
.
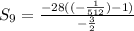 .
.
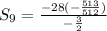 .
.
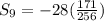 .
.
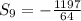 .
.
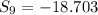 .
.
The correct answer is B