Question

Vince loads 10 boxes into his truck.Some of the boxes weigh 20 pounds, and some weigh 30 pounds.The total weight of the boxes is 280 pounds. If x= the number of 20-pound boxes and y= the number of 30-pound boxes, which pair of equations will give the number of 20-pound and 30-pound boxes Vince has?

Answer 1

No, Jude’s graph is incorrect. The inequality symbol is “less than,” so -9 is not included. He should have used an open circle on -9.Explanation:

2020 on eng

Answer 2

Here, x represents the number of 20-pound boxes and y represents the number of 30 pound boxes.

As per the given condition: Vince loads 10 boxes into his truck.Some of the boxes weigh 20 pounds, and some weigh 30 pounds and the total weight of the boxes is 280 pounds.

⇒ x+ y =10 .....[1]

and

20x+30y = 280 .....[2]

Multiply equation [1] by 20 we get;

`20(x+y) = 20\cdot 10`

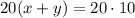
Using distributive property:
`a\cdot(b+c) = a\cdot b + a\cdot c`

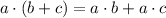
20x + 20y = 200 ....[3]

Subtract equation [3] from [2] we get;

`20x+30y-20x-20y = 280-200`

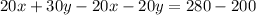
Combine like terms;

10y = 80

Divide both sides by 10 we get;

y = 8

Substitute this y value in equation [1] we get;

x + 8 = 10

Subtract 8 from both sides we get;

x + 8 -8 =10-8

Simplify:

x = 2

Therefore, the pairs of equation are: x+ y =10 and 20x+30y = 280

Vince has the number of 20-pound boxes is, 2 and the number of 30 pound boxes is, 8