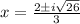What are the roots of 3x2 + 10 = 4x? Based on the attached image, is the answer either A, B, C or D?

Question

asked Dec 25, 2019 177k views

2 Answers

Javier Mr · Answer 1 · 2020-01-01T02:30:00+0000

Answer:

Option C is correct.

roots of the given equation ,
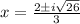
$x =(2\pm i√(26))/(3)$

Explanation:

Given the equation:

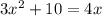
We can write this equation as:

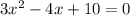
3x^2-4x + 10 =0

A quadratic equation is in the form of
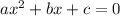......[1] where a,b ,c are the coefficient and x is the variable,

the solution of the equation is given by;

$x = (-b\pm√(b^2-4ac))/(2a)$

On comparing given equation with equation [1] we get;

a = 3 , b = -4 and c =10

So, the solution of the given equation is given by;

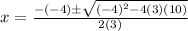
$x = (-(-4)\pm√((-4)^2-4(3)(10)))/(2(3))$

or

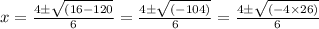
$x =  (4\pm√((16-120))/(6) = (4\pm√((-104)))/(6) = (4\pm√((-4 * 26)))/(6)$

or

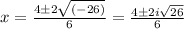$x =(4\pm2 √((-26)))/(6) = (4\pm2 i√(26))/(6)$ [∴
√(-1) = i

Simplify:

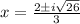
$x =(2\pm i√(26))/(3)$

therefore, the roots of the given equation are;
$x =(2\pm i√(26))/(3)$