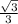Answer:
slope = -
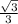
Explanation:
Differentiating implicitly with respect to x
2x + 2y
 = 0
= 0
2y
 = - 2x
= - 2x
 = -
= -
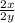 = -
= -

 is the measure of the slope of the tangent
is the measure of the slope of the tangent
rearrange equation to find corresponding y-coordinate of x = - 2
y² = 16 - 4 = 12 = 2
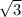 ⇒ y = ± 2
⇒ y = ± 2
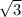
using x = - 2, y = - 2
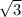 , then
, then
 = -
= -
 = -
= -