Question

Find an equation of a parabola with a vertex at the origin of directrix Y =
-2.5

Answer 1

`y=(1)/(10)x^2`

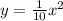
Explanation:

Since the directrix is
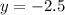`y=-2.5`, it means the axis of the parabola is parallel to the y-axis.

Also, the vertex is at the origin so the parabola opens upwards.

The equation of a parabola with these properties is of the form
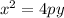`x^2=4py`, where
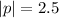`|p|=2.5`,that is the distance between the vertex and the directrix.

`\Rightarrow p=-2.5\:or\:2.5`.

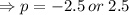Since the parabola opens upwards, we choose
`p=2.5`.

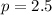The equation of the parabola now becomes,

`x^2=4(2.5)y`

`\Rightarrow x^2=10y`

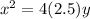
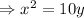
Or

`y=(1)/(10)x^2`

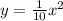
See graph