Question

What is the solution set of the equation, and why?
`(x-11)/(x+4)= 2-(4)/(x)`

A. {-8, 2}
B. {-16, 1}
C. {-1, 16}

Answer 1

B.) {-16,1}

Explanation:

First let us combine like terms so let us move the -4/x to the right side:

`(x-11)/(x+4)=2-(4)/(x)`

`(x-11)/(x+4) +(4)/(x)=2`

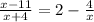
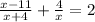
Let us find a common denominator for the left side by using :
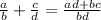`(a)/(b)+(c)/(d)=(ad+bc)/(bd)` and so:

`(x(x-11)+4(x+4))/(x(x+4)) = 2\\ \\(x^2-11x+4x+16)/(x^2+4x)=2\\`

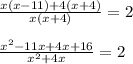
Now lets get rid of that fraction by multiplying both sides by
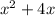`x^2+4x` and we obtain:

`x^2-7x+16=2(x^2+4x)\\\\x^2-7x+16=2x^2+8x`

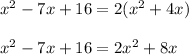
I'm going to move everything on the left side to the right by:
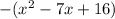`-(x^2-7x+16)` and so:

`0=2x^2+8x-x^2+7x-16\\\\0=x^2+15x-16`

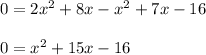
Now let's factor. We can factor by multiplying outer coefficients, so 1 x -16 = -16. Now let's list all the factors of 16: 1×16,8×2,4×4. From these factors try to find two that if you add or subtract them they will return the middle term of 15. So, 16 - 1 = 15. Therefore,

`0=x^2+15x-16\\\\0=x^2+16x-x-16\\\\0=x(x+16)-(x+16)\\0=(x-1)(x+16)`

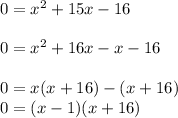
Now lets solve for both cases:

Case 1:

x-1=0

x=1

Case 2:

x+16=0

x=-16

and so your solutions are:

x={1,-16} or x={-16,1}

Answer 2

`Domain:\\x+4\\eq0\ \wedge\ x\\eq0\\\\\boxed{D:x\\eq-4\ \wedge\ x\\eq0}\\------------------------\\\\(x-11)/(x+4)=2-(4)/(x)\\\\(x-11)/(x+4)=(2x)/(x)-(4)/(x)\\\\(x-11)/(x+4)=(2x-4)/(x)\qquad\text{cross multiply}\\\\(x+4)(2x-4)=x(x-11)\qquad\text{use distributive property}\\\\(x)(2x)+(x)(-4)+(4)(2x)+(4)(-4)=(x)(x)+(x)(-11)\\\\2x^2-4x+8x-16=x^2-11x\\\\2x^2+(-4x+8x)-16=x^2-11x\\\\2x^2+4x-16=x^2-11x\qquad\text{subtract}\ x^2\ \text{from both sides}`

`x^2+4x-16=-11x\qquad\text{add}\ 11x\ \text{to both sides}\\\\x^2+15x-16=0\\\\x^2+16x-x-16=0\\\\x(x+16)-1(x+16)=0\\\\(x+16)(x-1)=0\iff x+16=0\ \vee\ x-1=0\\\\\boxed{x=-16\in D\ \vee\ x=1\in D}\\\\Answer:\ B.\ \{-16,\ 1\}`