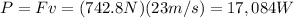(a) 11,500 W
The car is driving at constant speed on a horizontal surface. Constant speed means that the acceleration of the car is zero, so according to Newton's second law (F=ma), the net force must be zero.
We have two forces acting on the car: the driving force F, forward, and the drag force, D, acting backward. The net force must be zero, so:
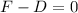
We know that D=500 N, so
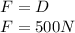
The power used by the engine is equal to the product between the force generated by the engine (F) and the velocity of the car (v=23 m/s), therefore:
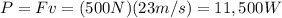
(b) 17,084 W
In this case, the car is moving on a hill with slope of
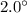 . Therefore, in this case, there is another force acting along the direction parallel to the surface: the component of the weight of the car parallel to the slope, which acts against the motion of the car. Its magnitude is given by:
. Therefore, in this case, there is another force acting along the direction parallel to the surface: the component of the weight of the car parallel to the slope, which acts against the motion of the car. Its magnitude is given by:
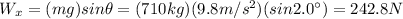
As before, the net force along the slope must be zero, since the car is moving at constant speed; therefore, the equation for the forces is
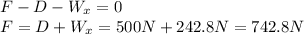
So, this time the power used by the engine is