2x 5 (mod 7) 4x 2 (mod 5) 3x 9 (mod 11) solve the above congruences - QAmmunity.org

2x 5 (mod 7) 4x 2 (mod 5) 3x 9 (mod 11) solve the above congruences

asked Nov 26, 2019 78.8k views

1 Answer

If you're supposed to solve the congruences one at a time:

1:
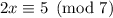
$2x\equiv5\pmod7$

First find the inverse of 5 modulo 7. Note that
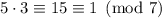$5\cdot3\equiv15\equiv1\pmod7$ , so
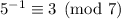$5^(-1)\equiv3\pmod7$ .

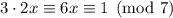
$3\cdot2x\equiv6x\equiv1\pmod7$

Then find the inverse of 6 modulo 7. Note that
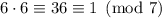$6\cdot6\equiv36\equiv1\pmod7$ , so 6 is its own inverse, and we have

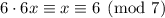
$6\cdot6x\equiv x\equiv6\pmod7$

so the first congruence has solution
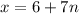x=6+7n where
$n\in\mathbb Z$ .

2:
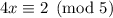
$4x\equiv2\pmod5$

We have
$3\cdot2\equiv6\equiv1\pmod5$ , so
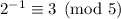$2^(-1)\equiv3\pmod5$ . Then

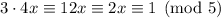
$3\cdot4x\equiv12x\equiv2x\equiv1\pmod5$

and

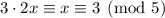
$3\cdot2x\equiv x\equiv3\pmod5$

so the solution is
x=3+5n for
$n\in\mathbb Z$ .

3:
$3x\equiv9\pmod{11}$

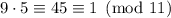$9\cdot5\equiv45\equiv1\pmod{11}$ , so
$9^(-1)\equiv5\pmod{11}$ , and

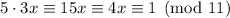
$5\cdot3x\equiv15x\equiv4x\equiv1\pmod{11}$

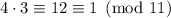$4\cdot3\equiv12\equiv1\pmod{11}$ , so
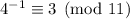$4^(-1)\equiv3\pmod{11}$ and

$3\cdot4x\equiv x\equiv3\pmod{11}$

so
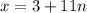x=3+11n for
$n\in\mathbb Z$ .

If they're to be taken simultaneously, use the Chinese remainder theorem.

Combined:

$\begin{cases}x\equiv6\pmod7\\x\equiv3\pmod5\\x\equiv3\pmod{11}\end{cases}$

Let's start with

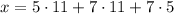
$x=5\cdot11+7\cdot11+7\cdot5$

so that two terms will vanish when considering the remainder of
modulo 7, 5, or 11, respectively.

Taken modulo 7, we have

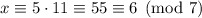
$x\equiv5\cdot11\equiv55\equiv6\pmod7$

Taken modulo 5, we have

$x\equiv7\cdot11\equiv77\equiv2\pmod5$

but we want to end up with 3, so we multiply the second term by the inverse of 2 modulo 5, then by 3. Note that
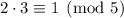$2\cdot3\equiv1\pmod5$ , so our new choice of
is

$x=5\cdot11+7\cdot11\cdot3\cdot3+7\cdot5$

and taken modulo 5, we end up with a remainder of 3, as desired.

Taken modulo 11, we have

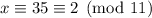
$x\equiv35\equiv2\pmod{11}$

but we want to end up with 3, so we multiply the third term by the inverse of 2 modulo 11, then by 3. Note that
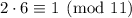$2\cdot6\equiv1\pmod{11}$ , so
becomes

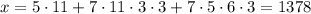
$x=5\cdot11+7\cdot11\cdot3\cdot3+7\cdot5\cdot6\cdot3=1378$

By the CRT, the least positive solution is

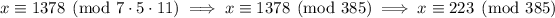
$x\equiv1378\pmod{7\cdot5\cdot11}\implies x\equiv1378\pmod{385}\implies x\equiv223\pmod{385}$

so the general solution to the system would be
x=223+385n for
$n\in\mathbb Z$ .

BarryWalsh answered Nov 30, 2019

7.8k points

Search QAmmunity.org