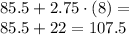Question

Can anybody help me w/ this ?

Answer 1

1. 42.3

When x=3 and y=7, the expression becomes

`3.6 x+4.5y =\\3.6\cdot (3) + 4.5\cdot (7) =\\10.8+31.5=42.3`

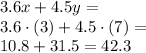
2. 32.6

When r=12 and s=4, the expression becomes

`5.5r-8.35 s=\\5.5\cdot (12)-8.35 \cdot (4)=\\(66)-(33.4)=32.6`

3.
`x(m)=12+0.5 m`

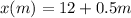
We can call
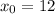`x_0=12` the initial weight of the object, and its weight increases by 0.5 for each month, so must add
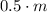`0.5\cdot m`. Therefore, the expression for the weight will be

`x(m)=12+0.5 m`

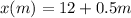
4. -11

For c = -2:

`4c-3 =\\4\cdot (-2)-3=\\(-8)-3=-11`

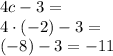
5. +3

For x = -6:

`(1)/(3)x+5=\\(1)/(3)\cdot (-6)+5=\\(-6)/(3)+5=\\-2+5=+3`

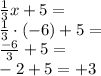
6. 14

For k = 20 and m = -2:

`0.3 k - 4 m=\\0.3 \cdot (20)-4 \cdot (-2)=\\(6)+(8)=14`

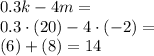
7. -60

For p = -26:

`-50+(5)/(13)p=\\-50 + (5)/(13)\cdot (-26)=\\-50 +(5\cdot (-26))/(13)=\\-50 - (5\cdot 2)=-50-10=-60`

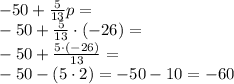
8.
`5.25b+6.5s`

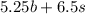
In fact, b represents the number of baseballs, while s represents the number of softballs. Each ball weights 5.25 ounces, so the total weigth of the baseballs is
`5.25 \cdot b`. Similarly, each softball weighs 6.5 ounces, so the total weight of the softballs will be
`6.5 \cdot s`

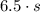
9. B. 157.5 pounds

The weight of the crate is 22.5 pounds.

The weight of each box is 11.25 pounds, and we have n=12 boxes, so the expression for the total weight will be

`w=22.5+ 11.25 n=\\22.5+11.25 \cdot 12=\\22.5+135=157.5`

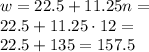
10.
`34 - 1.5 d`

We can assume that the initial amount of water in the container is 34 ounces. Every day, 1.5 ounces of water are lost: calling d the number of days, this means that after d days, we will have lost
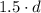`1.5\cdot d` ounces of water. Therefore, we must use a negative sign, and the final expression will be

`34 - 1.5 d`

11. 3.75 miles from the destination

The initial distance from the destination is d = 60. At each hour, the freigth covers a distance of 22.5 miles. Calling h the number of hours, the distance from the destination can be expressed as

`60-22.5 h`

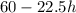
And substituting h = 2.5 (number of hours), we find the distance from the destination after 2.5 hours:

`60-22.5 \cdot (2.5)=\\60-56.25=3.75`

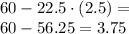
12. 107.5 feet

The initial elevation of the elevator is 85.5 feet. At each second, the elevation increases by 2.75 feet: if we call t the number of seconds passed, the elevation of the elevator can be expressed as

`85.5+2.75 t`

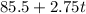
And substituting t=8 (number of seconds), we find the elevation after 8 seconds:

`85.5 + 2.75 \cdot (8)=\\85.5+22=107.5`