Question

An airplane travels 600 miles against the wind in 4 hours, and makes the return trip with then same wind in 2 hours. Find the speed of the wind.

Answer 1

The speed of wind is 75 miles / hour

Explanation:

Let's assume

speed of airplane is x miles /hour

speed of wind is y miles /hour

Against wind:

An airplane travels 600 miles against the wind in 4 hours

against wind means resultant speed will be less

so, speed =x-y

total distance traveled in 4 hour is

`=4(x-y)`

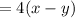
and this has to be equal to 600

`600=4(x-y)`

Divide both sides by 4

and we get

`x-y=150`

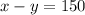
With wind:

makes the return trip with then same wind in 2 hours

with wind means resultant speed will be more

so, speed =x+y

total distance traveled in 2 hour is

`=2(x+y)`

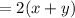
and this has to be equal to 600

`600=2(x+y)`

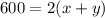
Divide both sides by 2

and we get

`x+y=300`

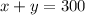
So, we get system of equations

`x-y=150`

`x+y=300`

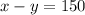
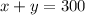
now, we can solve it by adding both equations

`x-y+x+y=150+300`

`2x=450`

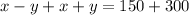
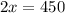
now, we can solve for x

`x=225`

now, we can find y by plugging x into any one equation

`225+y=300`

`y=75`

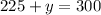
So,

The speed of wind is 75 miles / hour