Answer:
The mass of A and B together is 125kg
Step-by-step explanation:
To solve this problem, we set up the equations expressing the net force acting on A and B (forces acting to the right are +, those acting to the left are -):
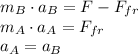
The net force acting on B is due to the acting pull force 100N less friction force caused by A. The net force on A is due to the friction force caused by the block B. Since we know both blocks accelerate at the same rate, the system can be solved easily:
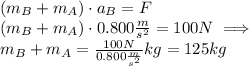
Of course, alternatively, in this very simple case you could consider A+B a single object being pulled with 100N, and obtain the same results by diving the pull force by the acceleration.