Answer:
The force of friction acting on block B is approximately 26.7N. Note: this result does not match any value from your multiple choice list. Please see comment at the end of this answer.
Step-by-step explanation:
The acting force F=75N pushes block A into acceleration to the left. Through a kinetic friction force, block B also accelerates to the left, however, the maximum of the friction force (which is unknown) makes block B accelerate by 0.5 m/s^2 slower than the block A, hence appearing it to accelerate with 0.5 m/s^2 to the right relative to the block A.
To solve this problem, start with setting up the net force equations for both block A and B:

where forces acting to the left are positive and those acting to the right are negative. The friction force F_fr in the first equation is due to A acting on B and in the second equation due to B acting on A. They are opposite in direction but have the same magnitude (Newton's third law). We also know that B accelerates 0.5 slower than A:
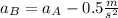
Now we can solve the system of 3 equations for a_A, a_B and finally for F_fr:
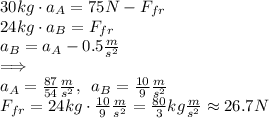
The force of friction acting on block B is approximately 26.7N.
This answer has been verified by multiple people and is correct for the provided values in your question. I recommend double-checking the text of your question for any typos and letting us know in the comments section.