Question

Assume that x has a normal distribution with the specified mean and standard deviation. Find the indicated probability. (Round your answer to four decimal places.)

μ = 14.3; σ = 3.7

P(10 ≤ x ≤ 26) =

Answer 1

0.8762 or 87.62%

Explanation:

Since our mean is μ=14.3 and our standard deviation is σ=3.7. If we're trying to figure out what percentage is P(10 ≤ x ≤ 26) equal to we must first calculate our z values as such:

`z=(x-\mu)/(\sigma)`

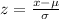
Our x value ranges from 10 to 26 therefore let x=10 and we obtain:

`z=(10-14.3)/(3.7) =-1.16\\`

If we look at our z-table we find that the probability associated with a z value of -1.16 is 0.1230 meaning 12.30%.

Now let's calculate the z value when x = 26 and so:

`z=(26-14.3)/(3.7)=3.16\\`

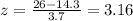
Similarly, we use the z-table again and find that the probability associated with a z value of 3.16 is 0.9992 meaning 99.92%.

Now we want to find the probability in between 10 and 26 so we will now subtract the upper limit minus the lower limit in P(10 ≤ x ≤ 26) therefore:

0.9992 - 0.1230 = 0.8762

or 87.62%