Question

1³+2³+...+2021³+2022³​

Answer 1

The following sum can be express to summation notation as
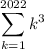`\displaystyle{\sum_(k=1)^(2022) k^3}`. We use Sigma to denote the sum of terms from intervals.

In order to find the sum, we will have to apply Summation Formula. Fortunately, the summation of cube term has its own formula which is:

`\displaystyle{\sum_(k=1)^n k^3 = \left[(n(n+1))/(2)\right]^2}`

Accorded to the formula, we will have to input the last term of series into the formula. Therefore, substitute n = 2022 in:

`\displaystyle{\sum_(k=1)^n k^3 = \left[(2022(2022+1))/(2)\right]^2}\\\\\displaystyle{\sum_(k=1)^n k^3 = \left[(2022(2023))/(2)\right]^2}\\\\\displaystyle{\sum_(k=1)^n k^3 = (1011\cdot 2023)^2}`

Evaluate the expression and we’ll get:

`\displaystyle{\sum_(k=1)^n k^3 = 4183059834009}`

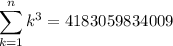
Hence, the sum is 4183059834009.

Please let me know if you have any questions!