Question

What force (in N) must be exerted on the master cylinder of a hydraulic lift to support the weight of a 2100 kg car (a large car) resting on the slave cylinder

Answer 1

Complete Question:

What force (in N) must be exerted on the master cylinder of a hydraulic lift to support the weight of a 2100 kg car (a large car) resting on the slave cylinder ? The master cylinder has a 2.00-cm diameter and the slave has a 24.0-cm diameter

Answer:

`F_1 = 142.92N`

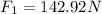
Step-by-step explanation:

Given

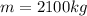`m = 2100kg` --- mass

`D_1 = 2.00\ cm` --- diameter of the large cylinder

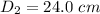`D_2 = 24.0\ cm` --- diameter of the slave cylinder

To do this, we apply Archimedes' principle of buoyancy which implies that:

`P = (F_1)/(A_1) = (F_2)/(A_2)`

Where

`F_1 = Force\ on\ the\ master\ cylinder`

`F_2 = Force\ on\ the\ slave\ cylinder`

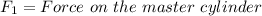
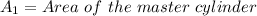
`A_1 = Area\ of\ the\ master\ cylinder`

`F_2 = Area\ of\ the\ small\ cylinder`

Calculating the area of the master cylinder.

`A_1 = \pi r_1^2`

`r_1 = (1)/(2)D_1 = (1)/(2) * 2.00cm = 1.00cm`

`A_1 = \pi* 1^2`

`A_1 = \pi * 1`

`A_1 = \pi`

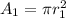
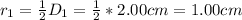
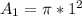
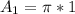
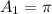
Calculating the area of the slave cylinder.

`A_2 = \pi r_2^2`

`r_2 = (1)/(2)D_2 = (1)/(2) * 24.00cm = 12.00cm`

`A_2 = \pi* 12^2`

`A_2 = \pi* 144`

`A_2 = 144\pi`

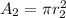
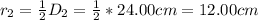
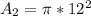
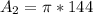
Substitute these values in:

`P = (F_1)/(A_1) = (F_2)/(A_2)`

`(F_1)/(\pi) = (F_2)/(144\pi)`

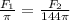
Multiply both sides by
`\pi`

`\pi * (F_1)/(\pi) = (F_2)/(144\pi) * \pi`

`F_1 = (F_2)/(144)`

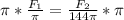
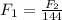
The force exerted on the slave cylinder (F2) is calculated as:

`F_2 = mg`

`F_2 = 2100 * 9.8`

`F_2 = 20580`

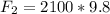
Substitute 20580 for F2 in
`F_1 = (F_2)/(144)`

`F_1 = (20580)/(144)`

`F_1 = 142.92N`

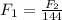
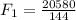
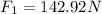
Hence, the force exerted on the master cylinder is approximately 142.92N