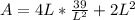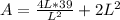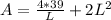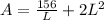Question

A closed box has a square base with side length feet and height feet. Given that the volume of the box is cubic feet, express the surface area of the box in terms of only.

Answer 1

Complete Question:

A closed box has a square base with side length L feet and height h feet. Given that the volume of the box is 39 cubic feet, express the surface area of the box in terms of L only.

Answer:

`A = (156)/(L) + 2L^2`

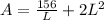
Explanation:

Given

`Volume = 39ft^3`

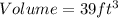
Required

Express the surface area in terms of L

Because the box has a square base:

The volume is:

`Volume = Base\ Area * Height`

Where

`Base\ Area = L * L`

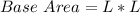
So, we have:

`Volume = L * L * H`

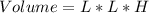
Substitute 39 for Volume

`39= L * L * H`

`39= L^2 * H`

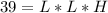
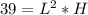
Make H the subject

`H = (39)/(L^2)`

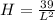
The surface area (A) of a box with square base is:

`A = 2(LH + LH + L^2)`

`A = 2(2LH + L^2)`

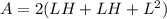
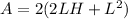
Open bracket

`A = 4LH + 2L^2`

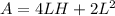
Substitute
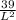`(39)/(L^2)` for H

`A = 4L * (39)/(L^2) + 2L^2`

`A = (4L *39)/(L^2) + 2L^2`

`A = (4*39)/(L) + 2L^2`

`A = (156)/(L) + 2L^2`