Question

A gas system has volume, moles and temperature of 9040 mL, 0.447 moles and -35.50 oC, respectively. What is the pressure in atm?

Answer 1

Answer : The pressure of the gas is, 0.964 atm

Solution : Given,

Volume of gas = 9040 ml = 9.040 L (1 L = 1000 ml)

Moles of gas = 0.447 moles

Temperature of gas =
`-35.50^oC=237.5K`
`(0^oC=273K)`

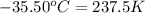
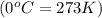
Using ideal gas equation,

`PV=nRT`

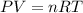
where,

P = pressure of the gas

V = volume of the gas

T = temperature of the gas

n = number of moles of gas

R = gas constant =
`0.0821Latm/moleK`

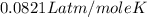
Now put all the given values in this formula, we get the pressure of the gas.

`P(9.040L)=(0.447moles)* (0.0821Latm/moleK)* (237.5K)`

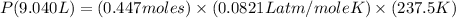
By rearranging the terms, we get

`P=0.964atm`

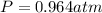
Therefore, the pressure of the gas is, 0.964 atm