Question

Use Newton's Law of Cooling, T = C + (T0 – C).ekt, to solve the problem. A cup of coffee with temperature 102°F is placed in a freezer with temperature 0°F. After 8 minutes, the temperature of the coffee is 52.5°F. What will its temperature be 13 minutes after it is placed in the freezer? Round your answer to the nearest degree.

Answer 1

35°F

Explanation:

`T= C + (T_0 - C)e^(kt)`

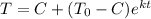
C is the temperature of environment = 0°F

T_0 is the initial temperature of object = 102°F

t is the time period = 8

Plug in all the values and solve for k

`T= 0 + (102 - 0)e^(k(8))`

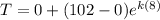
WE know T is 52.5°F after 8 minutes

solve for k

`52.5= 102e^(8k)`

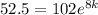
Divide both sides by 102

`(52.5)/(102) = e^(8k)`

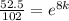
Take ln on both sides

`ln(52.5)/(102) = lne^(8k)`

`ln(52.5)/(102) = 8k`

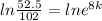
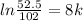
Divide both sides by 8

k=-0.08302

`T= 0 + (102 - 0)e^(k(t))`

Now we find out T when t= 13

`T= 0 + (102 - 0)e^(-0.08302(13))`

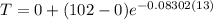
T= 34.66°F

So T= 35°F