Question

The sum of the first n terms of an A. P. is 2n and the sum of the first 2n terms is n. Find the sum of the first 4n terms.

Answer 1

The sum of first 4n terms is -10n.

Explanation:

The formula for sum of n terms of an AP is

`S_n=(n)/(2)[2a+(n-1)d]`

It is given that the sum of the first n terms of an A. P. is 2n and the sum of the first 2n terms is n.

`(n)/(2)[2a+(n-1)d]=2n`

`2a+(n-1)d=4` ..... (1)

`(2n)/(2)[2a+(2n-1)d]=n`

`2a+(2n-1)d=1` ..... (2)

Solve equation (1) and (2) by elimination method.

`d=-(3)/(n)`

`a=(1)/(2)(7-(3)/(n))`

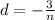
The sum of first 4n terms is

`S_(4n)=(4n)/(2)[2a+(4n-1)d]`

`S_(4n)=2n[2a+(4n-1)d]`

Put the value of a and d.

`S_(4n)=2n[2((1)/(2)(7-(3)/(n)))+(4n-1)(-(3)/(n))]`

`S_(4n)=2n[7-(3)/(n)-12+(3)/(n)]`

`S_(4n)=2n[-5]`

`S_(4n)=-10n`

Therefore the sum of 4n terms is -10n.