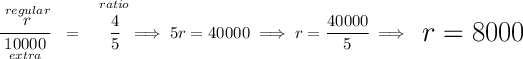Question

PLEASE ANSWER QEUSTION 2 I NEED IT BY TMR AND 8;15 A food company that produces peanut butter decides to try out a new version of its peanut butter that is extra crunchy, using twice the number of peanut chucks as normal. The company host a sampling of its new product at grocery stores and finds that 5 out of every 9 customers prefer that new extra crunchy version.

If the company normally sells a total of 90,000 containers of regular crunchy peanut butter, how many containers of new extra crunchy peanut butter should it produce, and how many containers of regular crunchy peanut butter should it produce? What would be helpful in solving this problem? Does one if our comparison statements above help us?

QEUSTION 2 if the company decides to produce 10,000 containers of new crunchy peanut butter, how many containers of regular crunchy peanut butter would it produce?

Answer 1

well, they found that 5 out of every 9 prefer the extra crunchy version, that means that 4 out of 9 didn't, meaning preferred the regular version, so we can say that the ratio of regular to extra crunchy is 4 : 5.

now, if the company holds to only sell 90000 containers, how many of each, using that ratio above, should they produce?

we can simply divide 90000 by (4 + 5) and then distribute accordingly.

`\stackrel{regular}{4}~~ : ~~\stackrel{extra}{5}\implies 4\cdot (90000)/(4+5)~ : ~5\cdot (90000)/(4+5)\implies {\LARGE \begin{array}{llll} \stackrel{regular}{40000}~~ : ~~\stackrel{extra}{50000} \end{array}}`

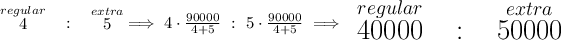
now, if the company decides to only produce 10000 containers of the new crunchy version, how many regular ones are there to produce, keeping in mind that 4 : 5 ratio?

`\cfrac{\stackrel{regular}{r}}{\underset{extra}{10000}} ~~ = ~~\stackrel{ratio}{\cfrac{4}{5}}\implies 5r=40000\implies r=\cfrac{40000}{5}\implies {\LARGE \begin{array}{llll} r=8000 \end{array}}`