Question

A parallelogram has sides 10m and 12m and an angle of 45°. Find the distance between the 12m-sides.

Answer 1

The distance between 12m-sides is
`5√(2)m`.

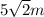Explanation:

It is given that the parallelogram has sides 10m and 12m and an angle of 45°.

Draw an altitude from one 12m side to another 12 m side as shown in below figure.

The opposite angles of parallelogram are same. Two angles are obtuse angles and two are acute angle.

Since angle C is acute angle therefore it must be 45 degree.

`\sin\theta=(perpendicular)/(hypotenuse)`

`\sin C=(BE)/(BC)`

`\sin(45^(\circ))=(d)/(10)`

`(1)/(√(2))=(d)/(10)`

`(10)/(√(2))=d`

`(10)/(√(2))* (√(2))/(√(2))=d`

`(10√(2))/(2)=d`

`5√(2)=d`

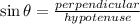
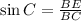
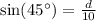
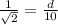
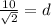
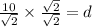
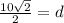
Therefore the distance between 12m-sides is
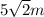`5√(2)m`.