Answer:
Last option is right
f(x) = one twentieth (x − 6)2 − 5
Explanation:
Given that it is a quadratic equation
Hence a parabola
Focus = (6,0)
Directrix is y =-10
Since vertex lies exactly in the middle from focus to directrix we have
vertex = (6,-5)
The parabola is having axis perpendicular to directrix and hence axis is x =6
The parabola is open up since focus lies above the directrix.
So equation is
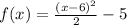
Hence last option is right
f(x) = one twentieth (x − 6)2 − 5