Question

Mario is writing a coordinate proof to show that the perpendicular bisector of an isosceles triangle base divides it into two triangles of equal area. Enter your answers in the boxes to complete Mario’s proof

Answer 1

x

0

x

x

y

Explanation:

Answer 2

The coordinates of D are (x,0). In triangle BCD the length of base is x. In triangle ABD the length of base is x and the height is y. The expression for the area is
`(1)/(2)xy`.

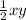Explanation:

From the given figure it is noticed that the vertices of triangle are A(0,0), B(x,y) and C(2x,0).

Since BD is a perpendicular bisector. Therefore the line BD divides the angle in two equal parts. It is given that triangle ABC is an isosceles triangle , therefore D bisects the segment AC.

So, D is midpoint of AC.

`Midpoint=((x_1+x_2)/(2),(y_1+y_2)/(2) )`

`D=((0+2x)/(2),(0+0)/(2))=(x,0)`

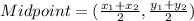
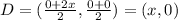
Therefore the coordinates of D are (x,0).

From the given figure it is notices that the base of the triangle is 2x and the height of the triangle is y. Area of triangle ABC is

`ABC=(1)/(2)* base* height`

`ABC=(1)/(2)* (2x)* y`

`ABC=xy`

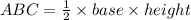
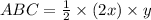
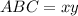
Therefore area of triangle ABC is xy.

From the figure it is noticed that the point D is midpoint therefore the measure of AD and DC is x.

In triangle ABD, the height of the triangle is yand the base of the triangle is x. So area of triangle ABD is

`ABD=(1)/(2)* (x)* y`

`ABD=(1)/(2)xy`

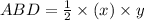
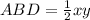
In triangle BCD, the height of the triangle is yand the base of the triangle is x. So area of triangle BCD is

`BCD=(1)/(2)* (x)* y`

`BCD=(1)/(2)xy`

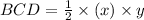
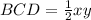
Therefore the area of both triangles are
`(1)/(2)xy`.

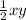Hence proved that the perpendicular bisector of an isosceles triangle base divides it into two triangles of equal area.