Question

Consider the function f(x)= 2/5x - 4

a. Find the inverse of and name it . Show and explain your work.
b. Use function composition to show that and are inverses of each other.
c.Draw the graphs of and on the same coordinate plane. Explain how your graph shows that the functions are inverses of each other

Answer 1

The inverse of the function is
`g(x)=(5)/(2)x+10`.

Explanation:

The given function is

`f(x)=(2)/(5)x-4`

`y=(2)/(5)x-4`

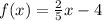
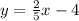
Interchange the variable x and y.

`x=(2)/(5)y-4`

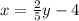
Now find the value of y in terms of x,

`x+4=(2)/(5)y`

`5(x+4)=2y`

`5x+20=2y`

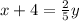
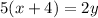
Divide both sides by 2.

`y=(5)/(2)x+10`

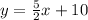
Put y=g(x)

`g(x)=(5)/(2)x+10`

Therefore the inverse of the function is
`g(x)=(5)/(2)x+10`.

If two function f and g are inverse of each other then
`(f\circ g)(x)=x`.

`(f\circ g)(x)=f(g(x))`

`(f\circ g)(x)=f((5)/(2)x+10)`

`(f\circ g)(x)=(2)/(5)((5)/(2)x+10)-4`

`(f\circ g)(x)=x+4-4`

`(f\circ g)(x)=x`

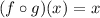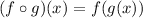
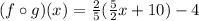
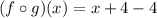
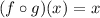
Therefore f(x) and g(x) are inverse of each other.

Graph of both functions are mirror image of each other across the line y=x, therefore functions are inverses of each other.