Question

Find the value of x if DE is the midsegment of triangle ABC and DE = 5x and BC = 11x – 15. Type the answer in the box below.

Answer 1

15

Explanation:

DE=5x

Bc=11x - 15

5x = 1/2 ( 11x - 15)

5x = 5.5x - 7.5

• Add 7.5 to both sides
• Then subtract 5 from both sides

7.5 = .5x

• Divide .05 on both sides

15 = x

Answer 2

Value of x is, 15

Explanation:

Given: DE = 5x and BC = 11x -15

Mid-segment theorem states that it connecting two sides of a triangle is parallel to the third side and is half as long.

In triangle ABC,

D is the midpoint of AB and E is the midpoint of AC as shown in the figure below.

So, DE is the mid-segment.

Therefore, by Mid-Segment theorem;

`DE = (1)/(2) BC`

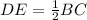
Substitute:

`5x = (1)/(2) 11x- 15`

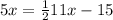
Multiply both sides by 2 we get;

`2 \cdot 5x = 2 \cdot (1)/(2) 11x- 15`

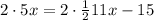
Simplify:

`10x = 11x- 15`

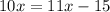
Subtract 11x from both sides we get

10x -11 x = 11x -15 - 11x

Simplify:

- x = -15

or

x = 15

Therefore, the value of x is, 15