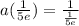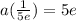Question

A particle is moving along the x-axis so that its position at t ≥ 0 is given by s(t)=(t)ln(5t). Find the acceleration of the particle when the velocity is first zero

5e
5e^2
e
None of these

Answer 1

`a((1)/(5e))=5e`

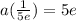
Explanation:

we are given equation for position function as

`s(t)=tln(5t)`

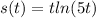
Since, we have to find acceleration

For finding acceleration , we will find second derivative

`s'(t)=(d)/(dt)\left(t\ln \left(5t\right)\right)`

`=(d)/(dt)\left(t\right)\ln \left(5t\right)+(d)/(dt)\left(\ln \left(5t\right)\right)t`

`=1\cdot \ln \left(5t\right)+(1)/(t)t`

`s'(t)=\ln \left(5t\right)+1`

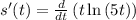
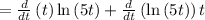
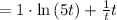
now, we can find derivative again

`s''(t)=(d)/(dt)\left(\ln \left(5t\right)+1\right)`

`=(d)/(dt)\left(\ln \left(5t\right)\right)+(d)/(dt)\left(1\right)`

`=(1)/(t)+0`

`a(t)=(1)/(t)`

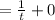
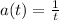
Firstly, we will set velocity =0

and then we can solve for t

`v(t)=s'(t)=\ln \left(5t\right)+1=0`

we get

`t=(1)/(5e)`

now, we can plug that into acceleration

and we get

`a((1)/(5e))=(1)/((1)/(5e))`

`a((1)/(5e))=5e`