Question

Jasmine bought 2 lb of ham and 1.5 lb of cheese from the deli and paid $7.25 she went back the following week and bought 3 lb of ham and 2 lb of cheese and Paid $10.50. if the prices remained the same find the price per pound of the ham and cheese

Answer 1

Given:

Jasmine bought 2 lb of ham and 1.5 lb of cheese from the deli and paid $7.25. She went back the following week and bought 3 lb of ham and 2 lb of cheese and Paid $10.50.

To Find:

The price per pound of the ham and cheese.

Answer:

The price per pound of ham is $2.5 and the price per pound of cheese is $1.5

Explanation:

Let the price per pound of ham be x and price per pound of cheese be y.

In her first trip, she bought 2lb of ham and 1.5lb of cheese and paid $7.25. This can be represented in terms of an equation as

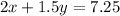`2x+1.5y=7.25` ...(1)

For the second trip, we can write

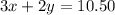`3x+2y=10.50` ...(2)

We can multiply the first equation by 3 and the second equation by 2 so that the coefficient of x in both is equal.

So we get

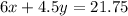`6x+4.5y=21.75` ...(3)

and

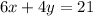`6x+4y=21` ...(4)

We can now subtract equation (4) from (3). We get

`0.5y=0.75`

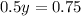
which means

`y=1.5`

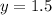
Substituting this value of y in (2),

`3x+2y=10.50\\\\3x=10.50-(2)(1.5)=10.50-3=7.5\\\\x=2.5`

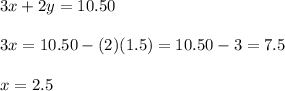
So, the price per pound of ham is $2.5 and the price per pound of cheese is $1.5