Question

Tickets for a concert cost $35 for balcony seats and $75 for floor seats. Tickets at the same venue for a theatrical production cost $25 for balcony seats and $60 for floor seats. If tickets for all the seats are sold, the venue generates $27,750 in revenue for a concert and $21,750 for a theatrical production. Which system of equations can be used to find the number of floor seats and balcony seats in the theater?

Answer 1

IT IS B I DID THE TEST

Explanation:

B:35 x + 75 y = 27,750. 25 x + 60 y = 21,750.

Answer 2

systems of equations by elimination and manipulation.

Explanation:

The systems of equations by elimination and manipulation method will help in this case find the number of seats there are in the theater.

We first need to create the equations.

Let x = number of balcony seats

Let y = floor seats

The equation for the concert will be:

35x + 75y = 27,750

The equation for the theatrical productions will be:

25x + 60y = 21,750

Now that we have our equations. Let's find a way to manipulate them to find the value of x and y.

35x + 75y = 27,750

25x + 60y = 21,750

In this case we need to find a way to eliminate either the x or y value by multiplying the equations with certain numbers.

Let's start by solving for x:

We can do this by multiplying the first equation by 4 and the second one by 5

4(35x + 75y = 27,750)

5(25x + 60y = 21,750)

Our new equations will be:

140x + 300y = 111,000

125x + 300y = 108,750

Now we can see the 300y on both equations can be eliminated if we subtract both equations to each other.

140x + 300y = 111,000

-125x + 300y = 108,750

15x + 0 = 2,250

`(15x)/(15) =(2,250)/(15)`

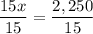
x = 150

Now that we have the value for x, we can then insert the value to any of the formulas that we created to find the value of y.

Let's use the equation 25x + 60y = 21,750.

25(150) + 60y = 21,750

3,750 + 60y = 21,750

60y = 21,750 + 3,750

`(60y)/(60)=(25,500)/(60)`

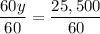
y = 425

So we have 150 Balcony seats and 425 Floor seats.