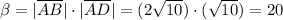You must to have that, the perimeter is the sum of the sides, and the area of a rectangle is the product of width by length.
So, the only that you need is calculate the measure of the sides.
For (a,b), (c,d) points in the plane, the distance between this two points is expressed by the following formula
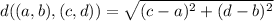
Perimeter:
P = (0,4), Q = (-2,0) , R = (2,0).
Let
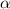 the perimeter, so
the perimeter, so
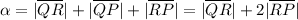
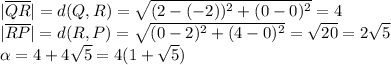
Area: Let
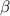 the area of the rectangle.
the area of the rectangle.
A = (-3,0), B =(3,2), D = (-2,3)