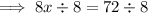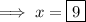Question

Can someone help me please?

Answer 1

(8x+9)° is co-interior with an angle vertical opposite with 99°

That makes it:

(8x+9)°+99°=180°(co-interior angles are supplementary)

`8x+108=180\\8x=180-108\\8x=72\\(8x)/(8) =(72)/(8) \\x=9`

Answer 2

`x=\boxed{9}`

`\textsf{Step 1}: \quad (8x + 9)^(\circ) + 99^(\circ) = \boxed{180}\;^(\circ)`

`\textsf{Step 2}: \quad 8x + \boxed{108} = \boxed{180}`

`\textsf{Step 3}: \quad 8x=\boxed{72}`

`\textsf{Step 4}: \quad x=\boxed{9}`

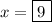
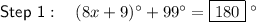
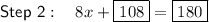
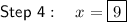
Explanation:

Alternative Exterior Angles Theorem

When a straight line intersects two parallel straight lines, the resulting alternate exterior angles are congruent.

Applying the Alternative Exterior Angles Theorem:

`\implies \angle 3 = 99^(\circ)`

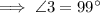
Step 1

Angles on a straight line sum to 180°.

`\implies (8x + 9)^(\circ) + \angle 3 = 180^(\circ)`

`\implies (8x + 9)^(\circ) + 99^(\circ) = \boxed{180}\;^(\circ)`

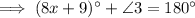
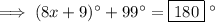
Step 2

Add the constants:

`\implies 8x+9+99=180`

`\implies 8x + \boxed{108} = \boxed{180}`

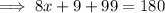
Step 3

Subtract 108 from both sides:

`\implies 8x+108-108=180-108`

`\implies 8x=\boxed{72}`

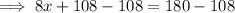
Step 4

Divide both sides by 8:

`\implies 8x / 8 = 72 / 8`

`\implies x=\boxed{9}`