Question

Can someone please help me with #5. Substitution method

Answer 1

Answer: the system of equations has no solution

Explanation:

`\displaystyle\\\left \{ {{-3x+3y=3} \atop {x-y=1}} \right. \ \ \ \ \Rightarrow\ \ \ \ \ \left \{ {{-3x+3y=3} \atop {x-y+y=1+y}} \right. \ \ \ \ \ \left \{ {{-3x+3y=3} \atop {x=1+y}} \right.\ \ \ \ \ \Rightarrow \\\\\\\left \{ {{-3x+3y=3} \atop {x-1=1+y-1}} \right.\ \ \ \ \ \Rightarrow\ \ \ \ \ \left \{ {{-3x+3y=3\ \ \ \ (1)} \atop {x-1=y\ \ \ \ (2)}} \right. \\`

Divide equation (1) by 3:

`\displaystyle\\\left \{ {{-x+y=1\ \ \ \ \ (3)} \atop {y=x-1\ \ \ \ \ (4)}} \right.`

Substitute equation (4) into equation (3):

`-x+x-1=1\\\\-1\\eq 1`

Hence, the system of equations has no solution

Answer 2

`x-y=1\\x=1+y........(3) equation`

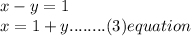
5.I derived the third equation from the second equation therefore I will substitute the above equation x=1+y in the first equation .Mind you to derive the third equation I made x the subject of the equation in the second equation. You can use any equation to derive the third equation. I chose to use the second equation because the variable have the coefficient of 1 so it will be very easier foe me without any divisions to leave the variable independent.

I will substitute the equation x=1+y in the equation -3x+3y=3.

If you derived the third equation from the second equation DO NOT substitute in the equation you derived the new equation from.

`-3(1+y)+3y=3\\-3-3y+3y=3\\-3\\eq 3`

as far as I went you can see that there is no solution for the first problem

No solution

6. Substitute y=-x+4 in the equation 2x-3y=3. In the place of y plug in-x+4

`2x-3(-x+4)=3\\\\2x+3x-12=3\\5x=3+12\\5x=15\\`

`(5x)/(5) =(15)/(5) \\x=3\\\\y=-(3)+4\\y=1`

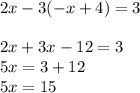
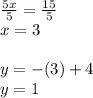
Hope this helps