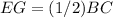Answer:
Part 1)
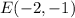 ,
,
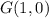
Part 2) slope EG is equal to slope BC (EG is parallel to BC)
Part 3)
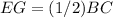
Explanation:
we have
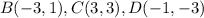
Step 1
Find the midsegment (EG) ̅ that is parallel to side (BC)
Find the x-coordinate of point E
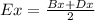
substitute
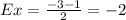
Find the y-coordinate of point E
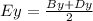
substitute
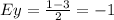
the coordinates of point E are
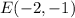
Find the x-coordinate of point G
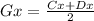
substitute
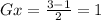
Find the y-coordinate of point G
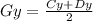
substitute
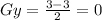
the coordinates of point G are
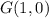
Step 2
Verifying EG is parallel to BC
we know that
If two lines are parallel, then their slopes are the same
The formula to calculate the slope between two points is equal to
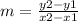
Find the slope EG
we have
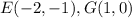
Substitute the values
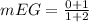
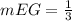
Find the slope BC
we have
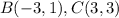
Substitute the values
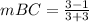
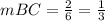
therefore
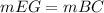 -------> EG is parallel to BC
-------> EG is parallel to BC
Step 3
Verifying
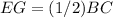
we know that
the formula to calculate the distance between two points is equal to
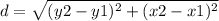
Find the distance EG
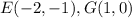
Substitute the values
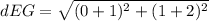
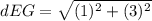
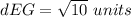
Find the distance BC
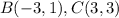
Substitute the values
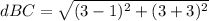
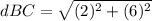
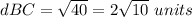
Verifying
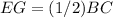
substitute the values
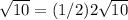
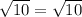 -------> is true
-------> is true
therefore