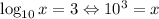Question

Exponential form of logx=3

Answer 1

`10^3 = x`

Explanation:

`\log_b x = y \Leftrightarrow b^y = x`

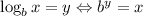
A logarithm is an exponent. For example, the log base 10 of 100 is the exponent you need to raise the base, 10, to get 100. It happens to be 2, so

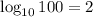`\log_(10) 100 = 2` can be written as
`10^2 = 100`

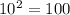
When you change log form to exponential form, keep these things in mind: The base of the log is also the base of the exponential form. The number that equals the log is the exponent. The number you take the log of is equal to the base raised to the exponent.

Now let's look at your problem.

`\log x = 3`

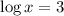
Since no base is shown, the base is 10.

`\log_(10) x = 3`

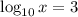
The base is 10. The exponent is 3. The base raised to the exponent equals x.

`\log_(10) x = 3 \Leftrightarrow 10^3 = x`