Question

What is a difference is squares that has a factor of x+8? Complete the expression

Answer 1

`\bf \textit{difference of squares} \\\\ (a-b)(a+b) = a^2-b^2 ~\hfill (x+8)\boxed{(x-8)}\implies x^2-8^2\implies x^2-64 \\\\\\ ~\hspace{34em}`

Answer 2

`(x^2-8^2)`

Explanation:

Here the question is asking to determine the difference of the squares , which has (x-8) has one of the factor.

Let us understand the formula for difference of the squares

`a^2-b^2=(a+b)(a-b)`

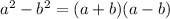
Here we can see that (a-b) is a factor of difference of squares too. Hence we substitute the values of a as x and b as 8 to find the answer.

`x^2-8^2=(x+8)(x-8)`

Hence our answer is
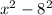`x^2-8^2` as it has (x-8) as one of its factor and it is a difference of squares .