Given equation is
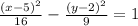
The given equation is in the form of
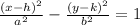
a^2= 16 , so a=4
b^2 = 9 so b= 4
The value of 'a' is greater than the value of 'b'
So it is a Horizontal hyperbola
First two graphs are horizontal hyperbola
Here center is (h,k)
h= 5 and k =2 from the given equation
So center is (5,2)
Now we find vertices
Vertices are (h+a,k) and (h-a,k)
We know h=5, k=2 and a=4
So vertices are (9,2) and (1,2)
Second graph having same vertices and center
The correct graph is attached below